Conditional Probability

Let  $E^c$  denote the complement of an event $E$. Let $E,F,G$ be pairwise independent events with  $P\left(G\right)>0$ and $P\left(E\cap F\cap G\right)=0$. Then  $P\left(E^c\cap F^c|G\right)$ equals 

Two fair dice are rolled. Let $X$ be the event that the first die shows an even number and $Y$ be the event that the second die shows an odd number. The two events $X$ and $Y$ are:

Suppose that
Box-I contains $8$ red, $3$ blue and $5$ green balls,
Box-ll contains $24$ red, $9$ blue and $15$ green balls,
Box-III contains $1$ blue, $12$ green and $3$ yellow balls,
Box-IV contains $10$ green, $16$ orange and $6$ white balls.
A ball is chosen randomly from Box-l; call this ball $b$. If $b$ is red then a ball is chosen randomly from Box-ll, if $b$ is blue then a ball is chosen randomly from Box-III, and if $b$ is green then a ball is chosen randomly from Box-IV. The conditional probability of the event 'one of the chosen balls is white' given that the event 'at least one of the chosen balls is green' has happened, is equal to

Four persons draw $4$ cards from an ordinary pack. If the chance that a card is of each suit is $p_1$ and the chance that no two cards are of equal value is $p_2$ then the value of $\frac{p_1}{p_2}=$

A bag initially contains one red and two blue balls. An experiment consisting of selecting a ball at random, noting its colour and replacing it together with an additional ball of the same colour. If three such trials are made, then:

$A$ and $B$ alternately throw a pair of dice. $A$ wins if he throws a sum $6$ before $B$ throws sum $7$ and $B$ wins if he throws a sum  $7$ before $A$ throws sum $6$. If $A$ starts the game, then

A fair coin is tossed three times and the following events are considered

$A=$ toss $1$ and toss $2$ produce different out comes

$B=$ toss $2$ and toss $3$ produce different out comes

$C=$ toss $3$ and toss $1$ produce different out comes Then

$A$ and $B$ try to hit a target. The probability that $A$ hits the target is $\frac{7}{10}$ and the probability that $B$ hits the target is $\frac{4}{10}.$ If these two events are independent, the probability that $B$ hits the target, given that the target is hit, is

If $A$ and $B$ are two independent events such that $P\left(A\right)=\frac{3}{10}$ and $P\left(A\cup B\right)=\frac{4}{5},$ then $P\left(A\cap B\right)$ is equal to

Jake and Elisa are given a mathematics problem. The probability that Jake can solve it is $0.35$. If Jake has solved it, the probability that Elisa can solve it is $0.6$. Otherwise, the probability that Elisa can solve it is $0.45$. Draw a tree diagram to illustrate the above question, showing clearly the probabilities on each branch. Find the probability that at least one of the students can solve the problem. 

Jake and Elisa are given a mathematics problem. The probability that Jake can solve it is $0.35$. If Jake has solved it, the probability that Elisa can solve it is $0.6$. Otherwise, the probability that Elisa can solve it is $0.45$. Draw a tree diagram to illustrate the above question, showing clearly the probabilities on each branch. Find the probability that Jake solves the problem, given than Elisa has.

Jake and Elisa are given a mathematics problem. The probability that Jake can solve it is $0.35$. If Jake has solved it, the probability that Elisa can solve it is $0.6$. Otherwise, the probability that Elisa can solve it is $0.45$. Draw a tree diagram to illustrate the above question, showing clearly the probabilities on each branch.

The Venn diagram illustrates the number of students taking each of the three sciences: physics, chemistry and biology.

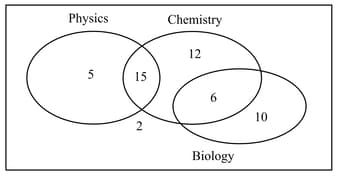
A student is randomly chosen from the group.

Find the probability that the student studies physics, given that they study chemistry. (Write answer in simplest fraction form)

A box contains four blue balls and three green balls. Judith and Gilles play a game with each taking it in turn to take a ball from the box, without replacement. The first player to take a green ball is the winner. Judith plays first. Find the probability that she wins. The game is now changed so that the ball chosen is replaced after each turn. Judith still plays first. Determine whether the probability of Judith winning has changed.

A box contains four blue balls and three green balls. Judith and Gilles play a game with each taking it in turn to take a ball from the box, without replacement. The first player to take a green ball is the winner. Judith plays first. Find the probability that she wins.

Hamid must drive through three sets of traffic lights in order to reach his place of work. The probability that the first set of lights is green is $0.7$. The probability that the second set of lights is green is $0.4$. The probability that the third set of lights is green is $0.8$. It may be assumed that the probability of any set of lights being green is independent of the others. Find the probability that at least one set of lights will be green.

Hamid must drive through three sets of traffic lights in order to reach his place of work. The probability that the first set of lights is green is $0.7$. The probability that the second set of lights is green is $0.4$. The probability that the third set of lights is green is $0.8$. It may be assumed that the probability of any set of lights being green is independent of the others.Given that first set of light is red and (i.e. not green), find the probability that the following two pairs of lights will be green.

Hamid must drive through three sets of traffic lights in order to reach his place of work. The probability that the first set of lights is green is $0.7$. The probability that the second set of lights is green is $0.4$. The probability that the third set of lights is green is $0.8$. It may be assumed that the probability of any set of lights being green is independent of the others. Find the probability that only one set of light is green.